对称加密中使用操作模式的动机

对称加密算法（如AES）也就是加密和解密过程使用相同的密钥key。本身只能安全加密固定大小的数据块。为了加密任意长度的消息，需要将这些基本算法运用在特定的操作模式中。

  • 一个块状密码可加密N bit的信息。如果不是N的整数倍，不是固定长度，或者类似TCP流呢？
  • 操作模式提供了使用区块密码加密灵活数据量的不同方法。

! CBC 和 CTR 符合 IND-CPA

确定性和完整性？

Deterministic确定性：同样的明文块会产生同样的密文块

Integrity完整性：确保数据在传输或存储过程中未被篡改的特性。如CTR就不是，因为CTR模式只提供加密功能，不包括验证数据未被改动的机制，也就不提供完整性校验。

ECB（电子密码本Electronic Code Book）模式：

使用块密码加密较长信息的最简单模式，将消息分割成块独立加密。其主要缺点是以相同的方式加密（Key k不变），所以同样的明文块会产生同样的密文块（这就是确定性），容易泄露信息。不推荐用。

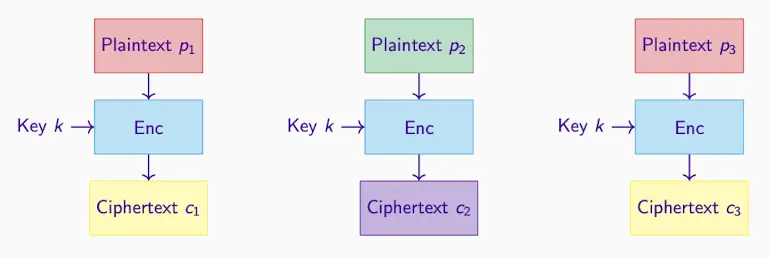
Screenshot_2024-03-10_at_05.25.11

  • 可能需要对最后一个块进行填充。
  • 填充容易出错，需要谨慎处理。块中出一点错整个块解密就错了。
  • 加密可以并行进行。
  • 加密是有确定性的，没完整性。
  • 很少用，特例：针对高熵明文空间的可搜索加密。

破解？

  • 建立密码本，弱密码易破解
  • 密码不变，再次出现就识别得到，如置换。

CBC（密码块链接Cipher Block Chaining）模式

在加密每个块（必须完整块，考虑填充）前，将它与前一个密文块进行XOR操作。这需要一个初始向量（IV）来启动过程。这增强了安全性，但仍然存在潜在的问题，如可预测的IV。

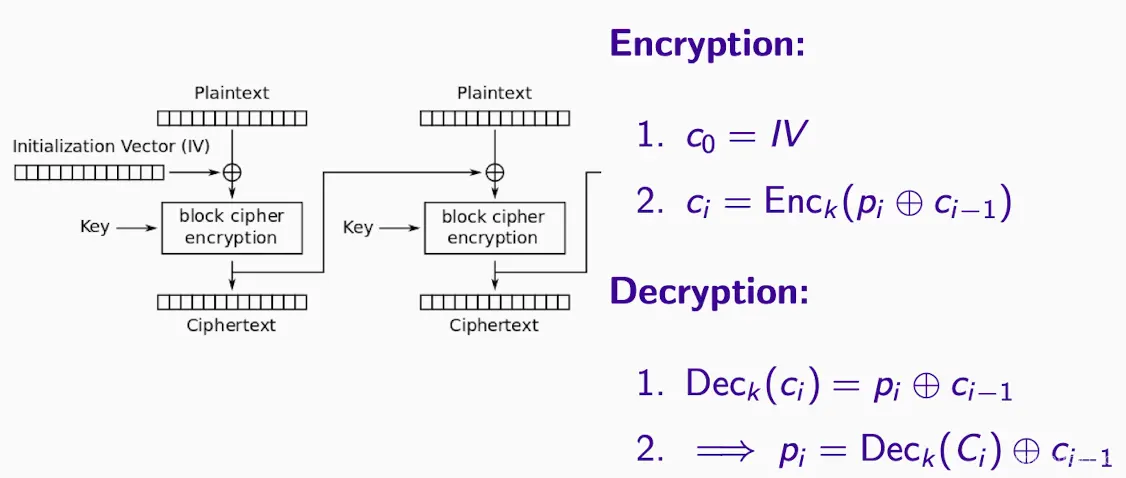
cipher_Block_Chaining

  • IV必须是均匀随机的，否则导致攻击
  • 没有确定性，没有完整性
  • 必须完整块N的倍数，可考虑填充，同时N太小会出问题
  • 必须使用不同密钥，同密钥多次加密密文块会导致碰撞ciphertext block collisions，即已知Pj就能恢复Pi，推倒如下：

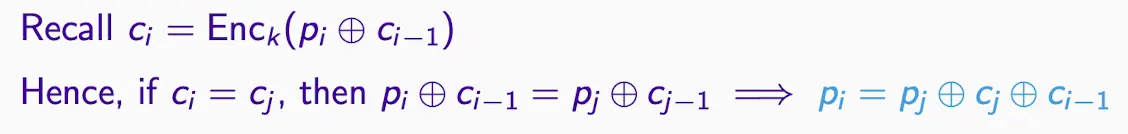
Screenshot_2024-03-10_at_05.38.45

CTR（计数器Counter）模式

将加密算法转换为流式加密器。它不直接加密消息，而是加密一个计数器（赋值不同），然后将输出与明文进行XOR操作。这提供了很高的灵活性和并行处理能力。

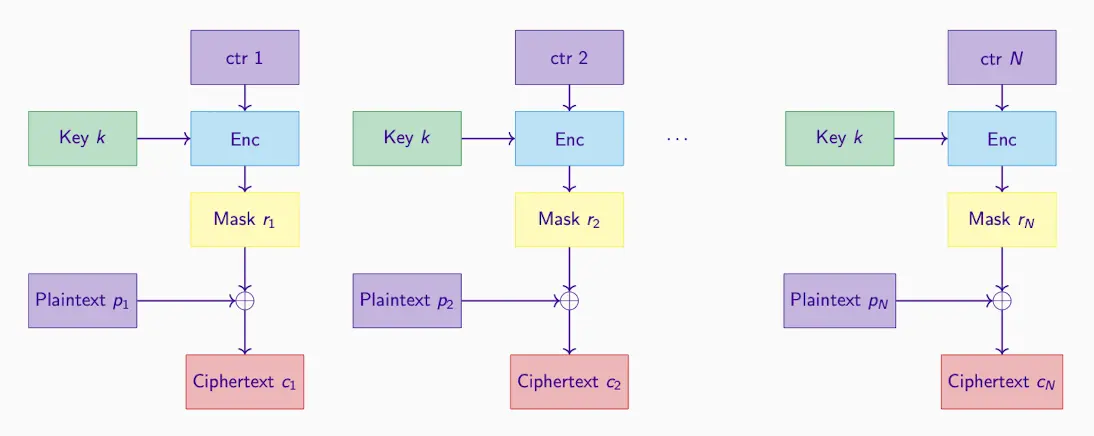
Screenshot_2024-03-10_at_05.51.31

  • 使用递增计数器 ctr 生成伪随机输出块（将位串 ctr 视为整数，加法 mod 2^n）。
  • 可并行运行。
  • 在知道明文之前预先计算加密掩码 Ri。
  • 快：分块密码通常比专用流密码设计要慢
  • 没有Integrity完整性，且所有流密码都如此。
  • 确定性
  • 不需要填充，因为最后一个输出块 rN 可以被截断为精确长度 pN。
  • 通常将 ctr 作为密文的一部分发送，如果解密过程可以通过其他方式恢复 ctr，我们可以省略 ctr。
  • 加密使用 Enc，解密也使用 Enc：
  • 因此，不需要实现 Dec -事实上，Enc 不需要可逆！
  • 从技术上讲，这意味着 CTR 模式可以使用一个伪随机function方法而不是伪随机排列permutation。

Key要求

密钥安全要求：对于固定的密钥 k，所有使用的计数器值（在所有加密中）必须是不同的。

  • 如果一个计数器是重复的，那么密文块的 XOR 将产生明文块的 XOR。
  • 类似于流密码的一次性密码笺/密钥流重复使用问题。

Error propagation 传播

  • 密文比特翻转bit-flip可能导致明文比特翻转。

步骤

使用不同计数器（ctr）值确保加密的唯一性，具体方法如下选一：

  1. 每次加密时ctr从0开始，更换密钥（成本较高）。
  2. 每次使用随机的ctr开始（需控制密钥使用以防碰撞）。
  3. 记录上次使用的ctr值，下次加1使用（需维护状态）。
  4. ctr由应用提供的固定大小的随机数（nonce N）和内部计数器组成，每次加密从0开始计数（防止nonce重复，限制明文大小以防内部计数器溢出）。
    此方法用于GCM模式（如下）。

GCM（伽罗瓦/计数器模式）

是CTR的变种，增加了数据完整性验证功能。它广泛用于保护网络数据，如TLS协议。

  • GCM 要求对每个加密和验证的数据块进行一次块密码运算和一次 128 位的乘法运算。
  • 确定性
  • 每个块密码操作都可并行化。
  • 由于加密与验证无关，软件实施可通过重叠验证和加密来提高速度。

对称加密的 IND-CPA 安全性

IND-CPA是认为对称加密算法安全的一个重要标准，通常通过引入随机性（如每次加密都使用不同的初始化向量IV）来实现。

四要素：KeyGen,Enc,Dec,Correctness

  • KeyGen: 均匀随机
  • Enc: key K + plaintext M → output C
    • 一般是随机的，如CBC、CTR
    • 后来的Enc可以有额外输入但要有确定性
  • Dec: key K + ciphertext C → output M or error
    • 假设有确定性，设可加密的最大明文长度为L，所以M 属于{0,1}≤L
  • Correctness: 求对于所有k
  • K is key space, M is message space, C is ciphertext space
  • 密文通常比明文长，但尽量短，减少拓展。

IND 不可区分性 Indistinguishable

这是一种安全属性，指的是给定两个不同的明文，加密算法产生的密文应该使攻击者无法确定哪个密文对应哪个明文（semantic security 语义安全）。理想情况下，即使攻击者知道或者可以选择明文，他们也无法从密文中获取任何有用信息。

CPA 选择明文攻击 Chosen Plaintext Attack

这是一种攻击模型，其中攻击者可以选择任意数量的明文并获得它们的密文。攻击者的目标是利用这些信息来破解加密算法，获取密钥或解密其他密文。

属性

  • IND-CPA 安全性可捕捉信息恢复攻击：任何能从 c 中恢复 m 的攻击者都可以转化为能破解 IND-CPA 安全性的攻击者。
  • IND-CPA 安全性可捕捉密钥恢复攻击：任何攻击者，只要给定一些密钥对（m, c ），就能恢复密钥 k、都可以转化为破坏 IND-CPA 安全性的攻击者。
  • IND-CPA 安全性确保明文的每一位都被隐藏起来。
  • 可以证明，如果使用 CBC 模式和 CTR 模式等方案，它们都符合 IND-CPA 安全性定义如果使用良好的块密码。

怎么猜测？

Screenshot_2024-03-10_at_19.07.37

Padding and padding oracle attacks

为何填充？

为了确保明文长度符合加密算法所需的固定块大小，防止在块加密中明文长度不足的问题。

  • 对于CBC模式，填充 - 加密 - 移除填充。
    • 但容易被攻击，可通过MAC实现完整性来检测修改过的密码文本，MAC需要和加密方案结合。
  • 可以是随机，也可以是确定的。
  • 需要是N的倍数的比特串。
  • 可拓展的。

简单例子对于AES的padding

对于AES算法，其中N = 128位，也就是N/8 = 16字节。因此，可能添加到消息中的填充字符串（以字节格式）是从0x01到0x0F，具体取决于需要填充的字节数。例如，如果你需要填充5个字节来达到下一个128位边界，那么每个填充字节的值将是0x04，因为0x04是十六进制表示的5减去1。

Screenshot 2024-03-10 at 20.47.25.png

填充要求

至少添加一个byte字节的填充: 为了使填充机制能够在解密时被识别和移除，即使消息的长度已经是加密算法所需的块大小的倍数，也至少添加一个字节的填充。
消息长度是N位的整数倍: 将添加一个完整的新块，仅包含填充。
安全性后果: 填充可能会引入安全风险，比如填充预测攻击（Padding Oracle Attack）。

错误传播

在对称加密中，一个错误的密文块会导致解密时该块完全错误，并影响下一个块的一部分，因为错误会在解密操作中传播。

full plaintext recovery attack 全明文恢复攻击

全明文恢复目标是从密文中恢复出明文信息,不一定需要恢复出密钥；它可能仅仅是解密出一个或多个密文。

Padding Oracle Attack 填充预言机攻击 is a chosen ciphertext attack

一种安全漏洞。

  • 如果 padding 不是预期值之一，则抛出异常，并给出有用的错误信息。
  • 它利用加密系统处理padding错误的方式来进行攻击。比如错误信息在网络或通过日志可见，或定时行为，会暴露。
  • 错误可能导致会话终止。
  • 密码文可能有额外限制。（最小/最大长度）
  • 属于chosen ciphertext attack CCA选择密文攻击（因为攻击者需要解密信息），因此不在 IND-CPA安全模型所涵盖。
  • 导致full plaintext recovery attack。
  • 每个字节8比特，8*16 = 128次尝试每字节。
  • 从块中的右向左目标字节，逐渐增加有效填充模式的长度。（参见前一页幻灯片）

例子中使用0x01，这表示当只差一位填充时。要根据缺少位数改变。

attack_process

Attack on CBC Mode with Predictable IVs

  • 可扩展到full plaintext recovery完全明文恢复
  • 多年来对 SSL/TLS 记录协议的首次重大攻击

BEAST Attack

  • JavaScript 需要能够在 SSL/TLS 记录协议信息的最开始注入其选择的明文块。

  • JavaScript 还需要与 MITM 攻击者通信。

  • 与同源策略有关的问题。

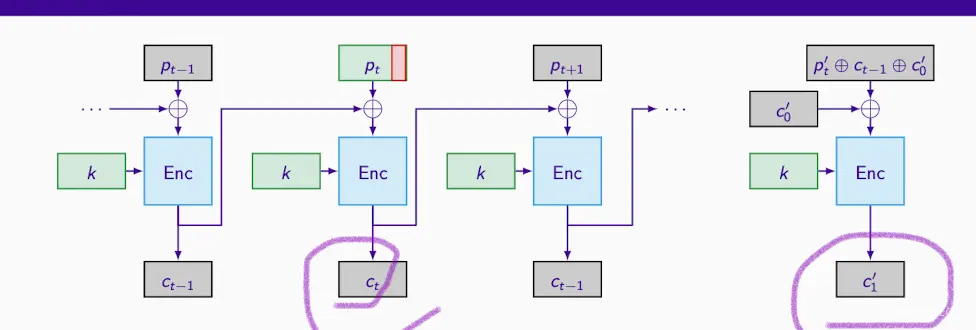
    Screenshot_2024-03-14_at_00.31.28

attack_process2

BEAST攻击的成功依赖于以下条件：

  • 攻击者能够在受害者的浏览器上运行他们的代码。
  • 使用了容易受到攻击的协议版本（SSL 3.0或TLS 1.0）。
  • 使用了可预测的IV（在TLS 1.0中，IV是前一个密文块，因此是可预测的）。

BEAST 的后果是什么？

  • BEAST 令 TLS 非常头疼。
  • 大多数客户端实施都 "停留 "在 TLS 1.0。
  • 最佳解决方案：升级到 TLS 1.1 或 1.2。
  • 使用随机 IV，因此可防止攻击。
  • 但也需要服务器端的支持。
  • 对于 TLS 1.0，有多种破解方法：
  • 客户端使用 1/n- 1 记录分割可以阻断攻击。- 在每条真实记录前发送长度为 0 的虚拟记录。- 或者改用 RC4？