哈希函数的介绍:
 !
!
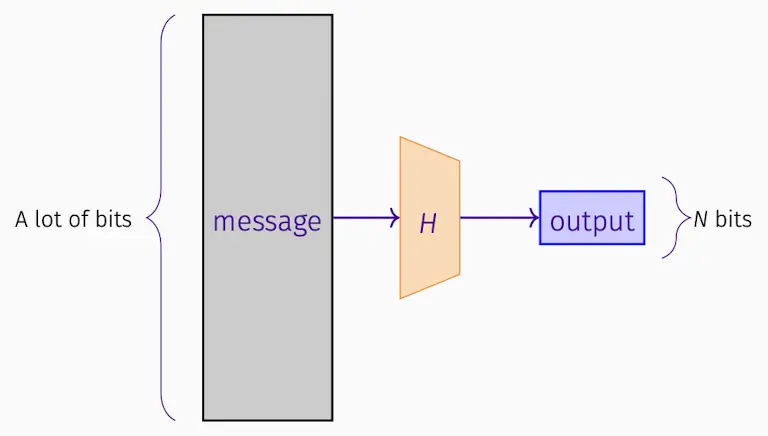
- 哈希函数是一种将任意长度输入字符串映射到固定长度哈希值(有时称为消息摘要)的高效可计算函数。不管输入几位,输出都是N bits。
- 哈希函数不是keyed primitive基于密钥的原语。
哈希函数的应用
包括message fingerprinting消息指纹生成、 file integrity checking文件完整性检查、signature schemes (hash-then-sign paradigm) 签名方案(先哈希后签名范式)、message authentication codes消息认证码(例如HMAC)、key derivation密钥派生(例如,在Diffie-Hellman密钥交换中从“原始数据”派生密钥)、password hashing密码哈希、commitment schemes承诺方案、pseudorandom number generators伪随机数生成器、stream ciphers流密码(计数器模式下的哈希函数)、bitcoin比特币(工作量证明方案)、post-quantum signature schemes后量子签名方案等。
哈希函数的标准:
NIST的SHA-1(直到2010年)、SHA-2(SHA-224、SHA-256、SHA-384、SHA-512)、SHA-3(Keccak);NESSIE的SHA-2(SHA-256、SHA-384、SHA-512)、WHIRLPOOL;CRYPTREC的SHA-2(SHA-256、SHA-384、SHA-512)。
password hashing密码哈希
加密散列函数可用于多种安全环境,但最著名的是密码hash。
- 服务器中密码是明文,服务器被入侵直接泄漏,攻击者冒充。
- 在数据库中只存储密码哈希值。
- 为每个用户存储 H(password) 而不是密码。
- 服务器对收到的密码进行Hash,并与表进行比较。匹配成功则验证成功。
- 直觉:攻击者必须逆向散列才能恢复密码。
Salting
- 在每次散列计算中添加一个随机的、账户专用的值,称为盐。
- 典型的盐值为 64 位,足够防止碰撞。
服务器存储 (salt, H(salt||password),而不是H(Password),salt时特定账户的随机值。
Iteration
- 典型的迭代次数: 10000,即每尝试一个密码都要算10000次,安全性更高。
哈希函数的安全属性
定理
碰撞:hash后的值相等,但hash前的值不等。
抗碰撞性意味着抗第二预映像性,任何collision resistance抗碰撞性的哈希函数都是second pre-image resistance抗第二预映像性的。
pre-image resistance抗预像和collision-resistance抗碰撞
-
pre-image resistance抗预像(单向性):有h不能找到m
-
second pre-image resistance抗二次预像:给定m1,若另一个m2的hash等于m1的hash,m2也不等于m1
-
collision resistance抗碰撞:在m对(pair)中,若有H(m1)=H(m2),m1也不等于m2
-
Near-Collision Resistance: hash值大部分相同的m1和m2也不相同,体现在信号中的公钥验证。
-
Partial Pre-Image Resistance 1:无法从给定hash值中恢复任何信息。
-
Partial Pre-Image Resistance 2:给定一个长度为l的hash值,无法在2l次尝试内获取到其message。


对于在 t 时间内运行的所有 A,A 输出碰撞的概率的边界是e

生日约束的含义
- N 位散列函数只能提供 N/2 位的安全性*,以抵御一般碰撞攻击。e.g. 我们需要 256 位输出的散列函数来实现 128 位的。
- 但目前还没有比一般生日攻击(2^128)更快的碰撞inding攻击。
- 在某些成本模型中,攻击成本为 2^(N/2) 个 "操作 "+内存。
普通散列函数并不好用(对于加密来说!)。非加密哈希函数(在加密方面)很弱!
Merkle-Damgård iterated hashing
-
用压缩函数 h 构建哈希函数。
-
将message分成固定长度为k的blocks (e.g. m1
, m2),其中包括了填充。 -
引入IV对m1
进行hash。。。然后引入m2重复步骤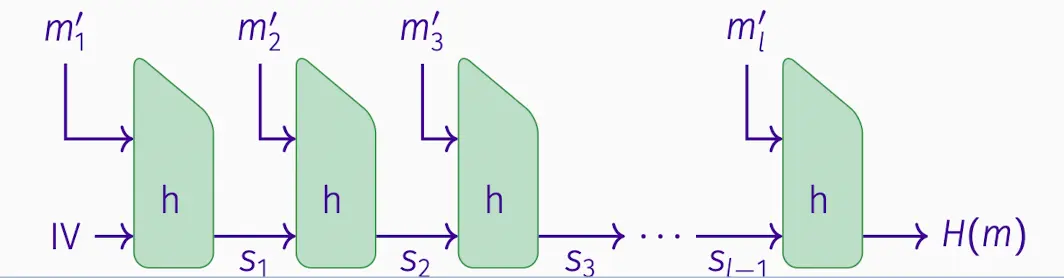
-
如果压缩函数 h 是抗碰撞的,那么 H 也是抗碰撞的。
length-extension 长度扩展特性
本来在tu就该输出了,但作为输入进入下一个块了。
在某些应用中存在问题,如 MAC 或密钥推导通过连接密钥和信息,从散列值函数构造出的函数。
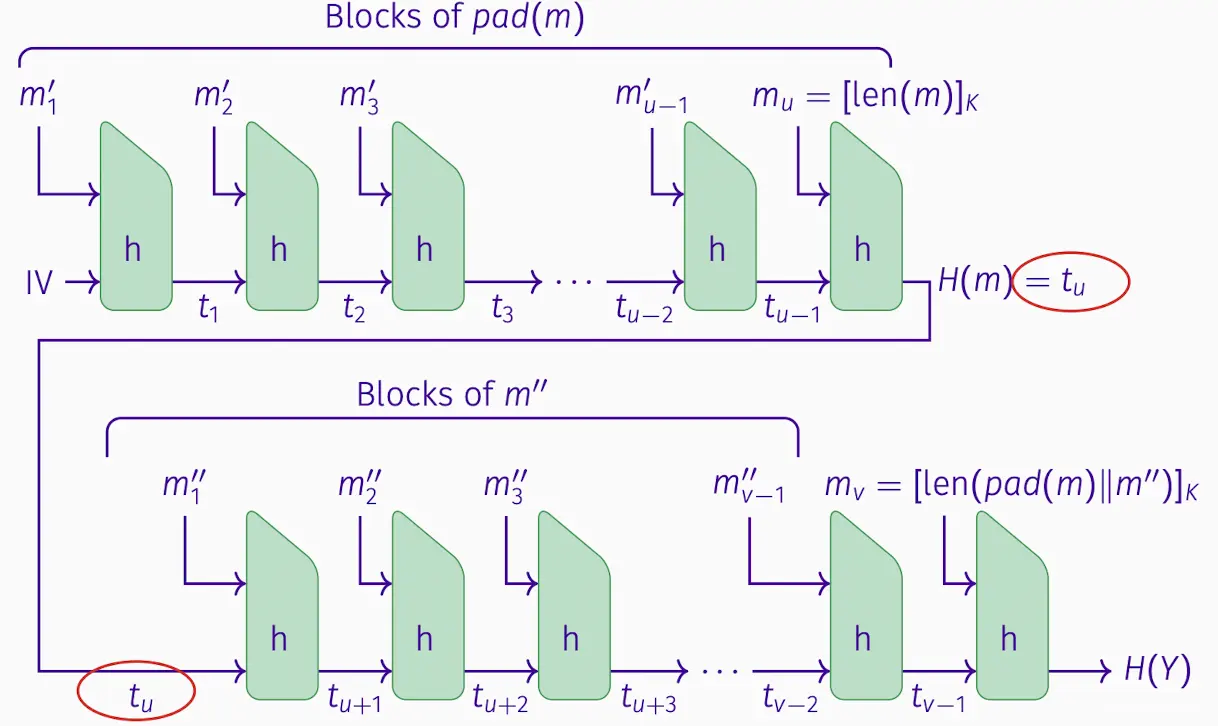
主要问题是散列输出大小 = 区块密码块大小,因此需要较大的块大小 N,以避免 2N/2生日攻击。
从块密码构建压缩函数
Davies-Meyer 戴维斯-迈耶:
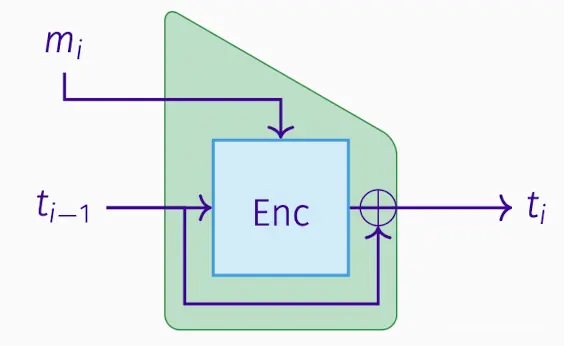
连锁变量变为信息输入;信息输入变为密钥。
给出了一种抗碰撞。
SHA-2
使用了戴维斯-迈耶模式的 256 位块密码建立压缩功能。
速度是SHA-1的两倍
SHA-3
允许可变长度输出,在密钥推导等应用中非常有用。
SHA3-256 比 SHA-256 稍慢(10-15%)。
Public Key Encryption (PKE)
公钥加密技术的基础是非对称加密机制,与传统的对称加密不同,非对称加密使用一对密钥:公钥和私钥。公钥用于加密信息,而私钥用于解密信息,这两个密钥是数学上相关联的,但是从公钥不能轻易计算出私钥,这就确保了信息传输的安全性。
三重算法:
- KGen: 随机key pair (sk,pk) sk is private key, pk is public key
- Enc: 一般是随机的, pk + m → c
- Dec: sk + c → m

过程
实际应用中不应该像教科书RSA这样直接使用。



破解关键点
- 不仅要保护秘密密钥难以猜测,更要确保信息的机密性,更确切地说,是在选择密文攻击(IND-CCA)下的不可区分性。
- 即使敌手能够获取任意消息的解密,也不应该有任何关于明文的信息泄露给敌手。
- 敌手能够访问加密和解密的预言机,分别用于密钥对(sk, pk)。
- 敌手可以提交任意消息对(m0, m1)到加密预言机,并接收加密消息c。
- 敌手还可以提交任意密文c’到解密预言机,并接收解密消息Dec_sk(c’)。
- 敌手的目标是恢复比特b。
- 这个定义与IND-CPA的定义进行了比较,但敌手在这里不能提交来自加密预言机的输出,否则他们可以轻易地赢得比赛。
IND-CCA选择密文攻击下的不可区分性
Indistinguishable (IND) under Chosen Ciphertext Attack
(CCA)

- 如果攻击者可以以某种方式从公钥(pk)恢复私钥(sk),该PKE方案就不是IND-CCA安全的。
- 一个方案是IND-CCA安全的,它必然是IND-CPA安全的
- 如果一个PKE方案有一个确定性加密算法,它就不是IND-CPA安全
- 教科书中的RSA是确定性的,所以它既不是IND-CPA安全也不是IND-CCA安全。在现实应用中,RSA需要采用像OAEP这样的填充方案来增加随机性,以达到IND-CPA和IND-CCA安全性。
使用例子
RSA 因数分解, ElGamal 离散对数, McEliece 基于代码的加密法, NTRUEncrypt 基于网格加密法
擅长?
- PIN code 如支付用
- 比对称加密贵
- PKE 通常用于传输对称密钥,用于加密批量或有效载荷数据。
- PKE 的这种用法通常被称为混合加密。
- 对称密钥在对称加密方案中用于加密实际数据。
关键封装机制KEM
体现了在选择密文攻击(CCA)下的不可区分性(IND),也称为IND-CCA安全性。

Hybrid Encryption混合加密
-
一般称为 KEM/DEM 范式。
-
简化了开发过程,因为开发者不需要配对加密原语,从而减少了复杂性和出错的可能性。
-
它利用密钥封装机制(KEM)来安全传输一个对称密钥,以及数据封装机制(DEM)来用对称密钥加密数据。

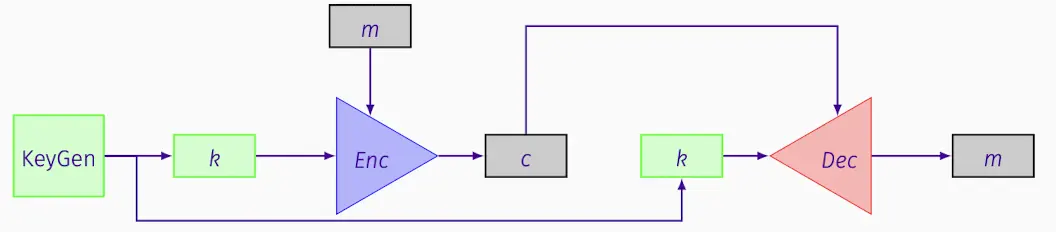
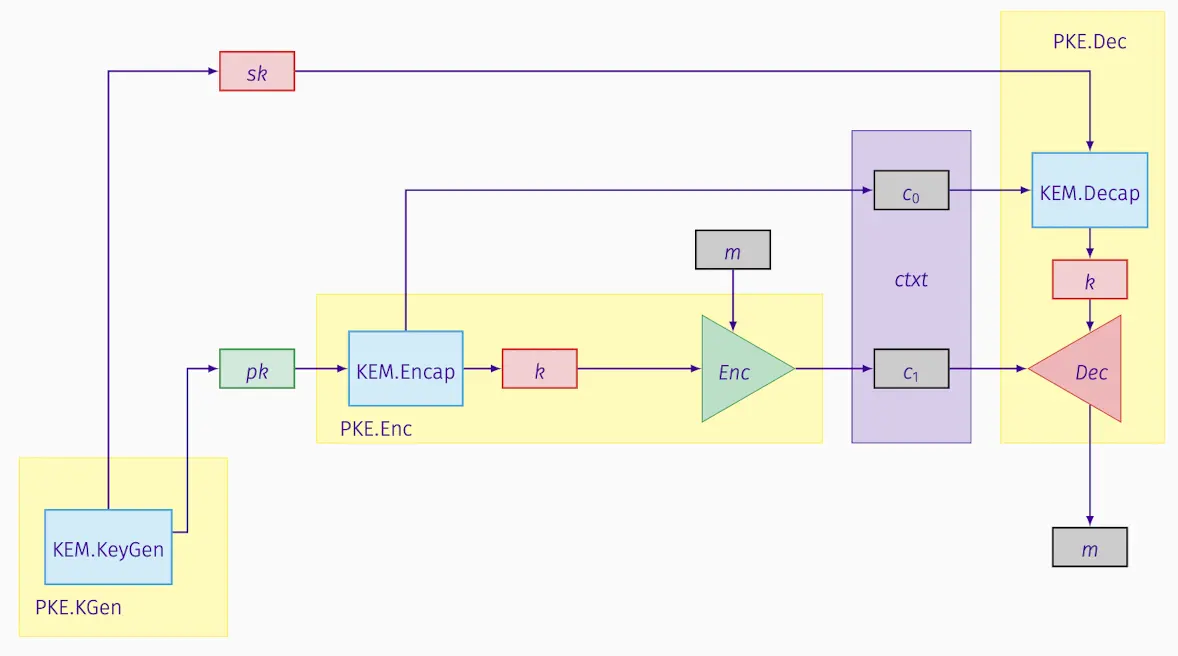
定理
PKE系统是从密钥封装机制(KEM)和数据封装机制(DEM)构建的,如果KEM是抗选择密文攻击(IND-CCA)安全的,同时DEM也是IND-CCA安全的,那么整个PKE系统也是IND-CCA安全的。
对称加密方案的核心问题在于需要预先共享加密密钥。为了解决这个难题,我们还有公钥加密机制。通过将PKE作为密钥封装机制来形式化使用,并且建立了混合加密,使用KEM/DEM范式,并展示如何证明其安全性。简要概括如下:
- 对称加密(SE)需要提前分享密钥,这在分布式环境中是不方便的。这就是为何需要引入公钥加密(PKE),它解决了密钥分发的问题。
- 然而,PKE相比于对称加密来说计算成本很高。为了保持效率,我们使用PKE加密一个较短的密钥,然后使用这个密钥通过对称加密(SE)来加密有效载荷数据。这种做法通常称为混合加密。
- 我们将PKE的使用形式化为密钥封装机制(KEM),并通过KEM/DEM范式构建混合加密,并展示如何证明其安全性。
总结来说,混合加密结合了PKE的安全性和SE的效率,通过密钥封装和数据封装两个步骤,以安全且高效的方式传输加密密钥和数据。

